CBSE Class 10 Maths Standard 2021 Question Paper
1. Write the quadratic equation in x whose roots are 2 and -5.
2. Find the exponent of 2 in the prime factorisation of 288.
3. (a) If α and β are the zeroes of the quadratic polynomial f(x) = x2 - x - 4, find the value of 1/α + 1/β - αβ.
OR
(b) If one zero of the quadratic polynomial x2 + 3x + k is 2, then find the value of k.
4. (a) If 3/5, a, 4 are three consecutive terms of an A.P., then find the value of a.
OR
(b) In an A.P., if the common difference d = -3 and the eleventh term a11 = 15, then find the first term.
5. A man goes 5 metres due West and then 12 metres due North. How far is he from the starting point ?
6. PQ is a tangent to a circle with centre O at the point P on the circle. If ΔOPQ is an isosceles triangle, then find ∠OQP.
7. Two concentric circles have radii 10 cm and 6 cm. Find the length of the chord of the larger circle which touches the smaller circle.
8. (a) If 3 sin A = 1, then find the value of sec A.
OR
(b) Show that :
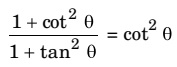
9. From a point on the ground, 20 m away from the foot of a vertical tower, the angle of elevation of the top of the tower is 60°. Find the height of the tower.
10. (a) Find the area of a circle whose circumference is 66 cm.
OR
The perimeter of a semi-circular protractor is 108 cm. Find its diameter.
11. Write the relationship between three measures of central tendency - Mean, Median and Mode.
12. In a ΔABC, if DE is parallel to BC, AD/DB = 4/5 and AC = 15 cm, then find the length of AE.
13. Simplify : cosec2 60° sin2 30° - sec2 60°
14. If tan θ + cot θ = 4√3/3, then find the value of tan2 θ+ cot2 θ.
15. If tangents PA and PB from an external point P to a circle with centre O are inclined to each other at an angle of 70°, then find ∠POA.
16. (a) How many outcomes are possible when three dice are thrown together ?
OR
(b) If P(E) = 0.015, then find P(not E).
Section II
Case study based questions (Q. No. 17 - 20) are compulsory. Attempt any 4 sub-parts from each question. Each sub-part carries 1 mark.
17. The residents of a housing society, on the occasion of environment day, decided to build two straight paths in the central park of the society and also plant trees along the boundary lines of each path.
Taking one corner of the park as origin and the two mutually perpendicular lines as the x-axis and y-axis, the paths were represented by the two linear equations 2x - 3y = 5 and 6x + 9y = 7.
Based on the above, answer the following questions :
(i) Two paths represented by the two equations here are
(A) intersecting
(B) overlapping
(C) parallel
(D) mutually perpendicular
(ii) Which one of the following points lie on the line 2x - 3y = 5 ?
(A) (-4, 1)
(B) (4, -1)
(C) (4, 1)
(D) (-4, -1)
(iii) If the line -6x + 9y = 7 intersects the y-axis at a point, then its coordinates are :
(A) (0, 7/9)
(B) (7/9, 0)
(C) (-7/6, 0)
(D) (0, -7/6)
(iv) If a pair of equations a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 has a unique solution, then
(A) a1/a2 = b1/b2 = c1/c2
(B) a1/a2 ≠ b1/b2
(C) a1/a2 = b1/b2 ≠ c1/c2
(D) a1/a2 ≠ b1/b2 ≠ c1/c2
(v) If a1/a2 = b1/b2 = c1/c2, then the two lines a1x + b1y + c1 = 0 and a2x + b2y + c2 = 0 are
(A) parallel
(B) coincident
(C) intersecting
(D) perpendicular to each other
18. Students of a school are standing in rows and columns in their school playground to celebrate their annual sports day. A, B, C and D are the positions of four students as shown in the figure.
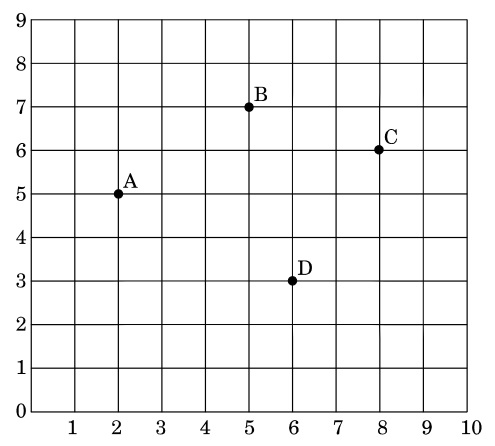
Based on the above, answer the following questions :
(i) The figure formed by the four points A, B, C and D is a
(A) square
(B) parallelogram
(C) rhombus
(D) quadrilateral
(ii) If the sports teacher is sitting at the origin, then which of the four students is closest to him ?
(A) A
(B) B
(C) C
(D) D
(iii) The distance between A and C is
(A) √(37) units
(B) √(35) units
(C) 6 units
(D) 5 units
(iv) The coordinates of the mid-point of line segment AC are
(A) (5/2, 11)
(B) (5/2, 11/2)
(C) (5, 11/2)
(D) (5, 11)
(v) If a point P divides the line segment AD in the ratio 1 : 2, then coordinates of P are
(A) (8/3, 8/3)
(B) (10/3, 13/3)
(C) (13/3, 10/3)
(D) (16/3, 11/3)
19. During the annual sports meet in a school, all the athletes were very enthusiastic. They all wanted to be the winner so that their house could stand first. The instructor noted down the time taken by a group of students to complete a certain race. The data recorded is given below :

Based on the above, answer the following questions :
(i) What is the class mark of the modal class ?
(A) 60
(B) 70
(C) 80
(D) 140
(ii) The mode of the given data is
(A) 70.33
(B) 71.33
(C) 72.33
(D) 73.33
(iii) The median class of the given data is
(A) 20 - 40
(B) 40 - 60
(C) 80 - 100
(D) 60 - 80
(iv) The sum of the lower limits of median class and modal class is
(A) 80
(B) 140
(C) 120
(D) 100
(v) The median time (in seconds) of the given data is
(A) 65.7
(B) 85.7
(C) 45.7
(D) 25.7
20. During summer break, Harish wanted to play with his friends but it was too hot outside, so he decided to play some indoor game with his friends. He collects 20 identical cards and writes the numbers 1 to 20 on them (one number on one card). He puts them in a box. He and his friends make a bet for the chances of drawing various cards out of the box. Each was given a chance to tell the probability of picking one card out of the box.
Based on the above, answer the following questions :
(i) The probability that the number on the card drawn is an odd prime number, is
(A) 3/5
(B) 2/5
(C) 9/20
(D) 7/20
(ii) The probability that the number on the card drawn is a composite number is
(A) 11/20
(B) 3/5
(C) 4/5
(D) 1/2
(iii) The probability that the number on the card drawn is a multiple of 3, 6 and 9 is
(A) 1/20
(B) 1/10
(C) 3/20
(D) 0
(iv) The probability that the number on the card drawn is a multiple of 3 and 7 is
(A) 3/10
(B) 1/10
(C) 0
(D) 2/5
(v) If all cards having odd numbers written on them are removed from the box and then one card is drawn from the remaining cards, the probability of getting a card having a prime number is
(A) 1/20
(B) 1/10
(C) 0
(D) 1/5
Part B
Section III
All questions are compulsory. In case of internal choices, attempt any one.
21. (a) Check whether the points P(5, -2), Q(6, 4) and R(7, -2) are the vertices of an isosceles triangle PQR.
OR
(b) Find the ratio in which P(4, 5) divides the join of A(2, 3) and B(7, 8).
22. (a) The sum of the numerator and the denominator of a fraction is 18. If the denominator is increased by 2, the fraction reduces to 1/3. Find the fraction.
OR
(b) Find the value of k for which the system of equations x + 2y = 5 and 3x + ky + 15 = 0 has no solution.
23. Explain why 2 x 3 x 5 + 5 and 5 x 7 x 11 + 7 x 5 are composite numbers.
24. Find the mean of first 10 composite numbers.
25. ABC is right triangle, right-angled at B, with BC = 6 cm and AB = 8 cm. A circle with centre O and radius r cm has been inscribed in ΔABC as shown in the figure. Find the value of r.
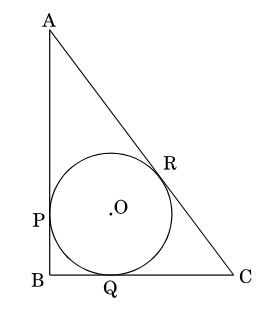
26. Draw a circle of radius 5 cm. From a point 8 cm away from its centre, construct a pair of tangents to the circle.
Section IV
27. Divide the polynomial f(x) = 5x3 + 10x2 - 30x - 15 by the polynomial g(x) = x2 + 1 + x and hence, find the quotient and the remainder.
28. Prove that 3 + √2 is an irrational number, given that 2 is an irrational number.
29. In the given figure, PT and PS are tangents to a circle with centre O, from a point P, such that PT = 4 cm and ∠TPS = 60°. Find the length of the chord TS. Also, find the radius of the circle.
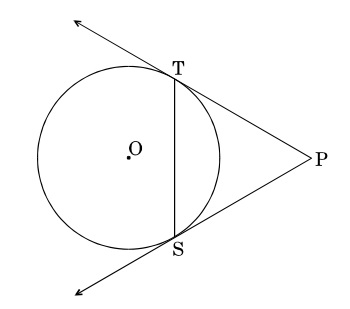
30. The areas of two similar triangles are 121 cm2 and 64 cm2 respectively. If one median of the first triangle is 12.1 cm long, then find the length of the corresponding median of the other triangle.
31. (a) Prove :
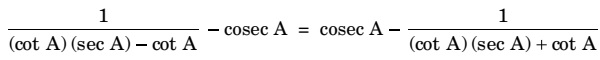
OR
(b) Prove :
sin6 A + 3 sin2 A cos2 A = 1 - cos6 A
32. (a) One root of the quadratic equation 2x2 - 8x - k = 0 is 5/2. Find the value of k. Also, find the other root.
OR
(b) Using quadratic formula, solve the following equation for x :
abx2 + (b2 - ac)x - bc = 0
33. With vertices A, B and C of a triangle ABC as centres, arcs are drawn with radii 2 cm each as shown in the figure. If AB = 6 cm, BC = 8 cm and AC = 10 cm, then find the area of the shaded region.
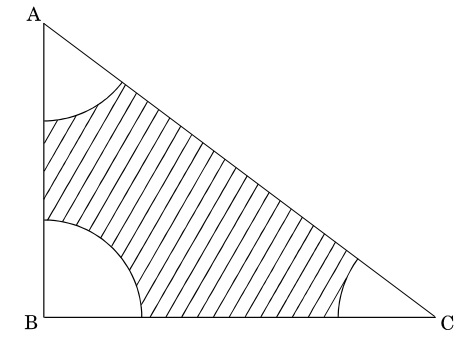
Section V
34. Water is being pumped out through a circular pipe whose internal diameter is 8 cm. If the rate of flow of water is 80 cm/s, then how many litres of water is being pumped out through this pipe in one hour ?
35. (a) A man on the top of a vertical tower observes a car moving at a uniform speed coming directly towards it. If it takes 18 minutes for the angle of depression to change from 30° to 60°, how soon after this will the car reach the tower ?
OR
(b) A girl on a ship standing on a wooden platform, which is 50 m above water level, observes the angle of elevation of the top of a hill as 30° and the angle of depression of the base of the hill as 60°. Calculate the distance of the hill from the platform and the height of the hill.
36. If Sn denotes the sum of first n terms of an A.P., prove that S12 = 3 (S8 - S4).